概要：.⑷共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.与互为共轭双曲线，它们具有共同的渐近线：.⑸共渐近线的双曲线系方程：的渐近线方程为如果双曲线的渐近线为时，它的双曲线方程可设为.例如：若双曲线一条渐近线为且过，求双曲线的方程？解：令双曲线的方程为：，代入得.⑹直线与双曲线的位置关系：区域①：无切线，2条与渐近线平行的直线，合计2条；区域②：即定点在双曲线上，1条切线，2条与渐近线平行的直线，合计3条；区域③：2条切线，2条与渐近线平行的直线，合计4条；区域④：即定点在渐近线上且非原点，1条切线，1条与渐近线平行的直线，合计2条；区域⑤：即过原点，无切线，无与渐近线平行的直线.小结：过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有0、2、3、4条.（2）若直线与双曲线一支有交点，交点为二个时，求确定直线的斜率可用代入法与渐近线求交和两根之和与两根之积同号.⑺若P在双曲线，则常用结论1：P到焦点的距离为m = n，则P到两准线的距离比为m︰n. 简证： = .常用结论2：从双曲线一个焦点到另一条渐近线的距离等于b.

高中数学知识点：双曲线方程总结,标签：高一数学课本|基础知识|教案,http://www.51jxk.com
.
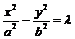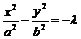⑷共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.与互为共轭双曲线，它们具有共同的渐近线：.
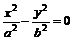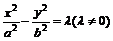⑸共渐近线的双曲线系方程：的渐近线方程为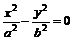如果双曲线的渐近线为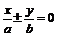时，它的双曲线方程可设为.
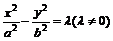例如：若双曲线一条渐近线为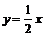且过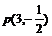，求双曲线的方程？
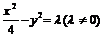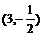解：令双曲线的方程为：，代入得.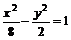
⑹直线与双曲线的位置关系：
区域①：无切线，2条与渐近线平行的直线，合计2条；
区域②：即定点在双曲线上，1条切线，2条与渐近线平行的直线，合计3条；
区域③：2条切线，2条与渐近线平行的直线，合计4条；
区域④：即定点在渐近线上且非原点，1条切线，1条与渐近线平行的直线，合计2条；
区域⑤：即过原点，无切线，无与渐近线平行的直线.
小结：过定点作直线与双曲线有且仅有一个交点，可以作出的直线数目可能有0、2、3、4条.
（2）若直线与双曲线一支有交点，交点为二个时，求确定直线的斜率可用代入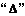法与渐近线求交和两根之和与两根之积同号.
⑺若P在双曲线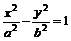，则常用结论1：P到焦点的距离为m = n，则P到两准线的距离比为m︰n. 
简证：  = .
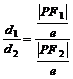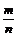常用结论2：从双曲线一个焦点到另一条渐近线的距离等于b. 

上一页  [1] [2]